Snells lov

En plan lysbølge bevæger sig fra ét medium (gult) til et andet (blåt) med forskellige brydningsindekser, hvorfor vinklen ændres.

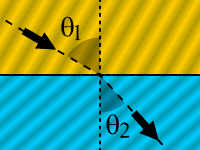
Snells lov beskriver, hvordan en lysbølge ændrer retning, når den går fra ét medium til et andet. For en grænseflade mellem medierne 1 og 2 gælder det, at:

$n_1\sin {\theta }_1=n_2\sin {\theta }_2$

hvor $n_1$ og $n_2$ er de respektive brydningsindekser, ${\theta }_1$ er indfaldsvinklen, og ${\theta }_2$ er den udgående vinkel. Det ses, at vinklerne er ens, hvis brydningsindekserne er ens, eller hvis indfaldsvinkel er nul. For meget små vinkler, kan loven approksimativt skrives som:

$n_1{\theta }_1=n_2{\theta }_2$

Det er tilfældet, hvis lyset er tæt på vinkelret på grænsefladen.

Snells lov er opkaldt efter Willebrord Snellius, men blev oprindeligt formuleret af perseren Ibn Sahl i 984.

Udledning

Illustration af Snells lov når den udledes med Fermats princip.

Snells lov kan udledes vha. Fermats princip. En lysstråle rejser fra punktet $Q$ i medium 1 til punktet $P$ i medium 2. I følge Fermats princip vil lysstrålen følge den vej, der tager kortest tid. Hvis de to medier var ens, ville dette være en lige linje, men forskellige brydningsindekser giver forskellig fart $v$ i de to medier:

$\begin{array}{cc}{v}_1& =\frac{c}{n_1}\\ v_2& =\frac{c}{n_2}\end{array}$

hvor $c$ er lysets fart i vakuum. Vejlængden $d$ igennem hvert medium er givet ved (se illustration):

$\begin{array}{cc}{d}_1& =\sqrt{a^2+x^2}\\ d_2& =\sqrt{b^2+(L-x{)}^2}\end{array}$

hvor $x$ angiver, hvor lysstrålen rammet grænsefladen. At komme fra $Q$ til $P$ tager altså tiden $t$:

$\begin{array}{cc}t& =\frac{d_1}{v_1}+\frac{d_2}{v_2}\\ t& =\frac{n_1}{c}\sqrt{a^2+x^2}+\frac{n_2}{c}\sqrt{b^2+(L-x{)}^2}\end{array}$

Ved at sætte den afledte mht. $x$ til 0, kan vejen med den korteste tid findes:

$\begin{array}{cc}\frac{dt}{dx}& =\frac{n_1}{2c}\frac{2x}{\sqrt{a^2+x^2}}-\frac{n_2}{2c}\frac{2(L-x)}{\sqrt{b^2+(L-x{)}^2}}=0\\ \frac{n_1}{2c}\frac{2x}{\sqrt{a^2+x^2}}& =\frac{n_2}{2c}\frac{2(L-x)}{\sqrt{b^2+(L-x{)}^2}}\\ n_1\frac{x}{\sqrt{a^2+x^2}}& =n_2\frac{L-x}{\sqrt{b^2+(L-x{)}^2}}\end{array}$

Vinklerne er givet ved:

$\begin{array}{cc}\sin {\theta }_1& =\frac{x}{\sqrt{a^2+x^2}}\\ \sin {\theta }_2& =\frac{L-x}{\sqrt{b^2+(L-x{)}^2}}\end{array}$

Når dette indsættes, findes Snells lov:

$n_1\sin {\theta }_1=n_2\sin {\theta }_2$