Indhylningskurve

En familie af lige linjer samt den resulterende indhylningskurve.

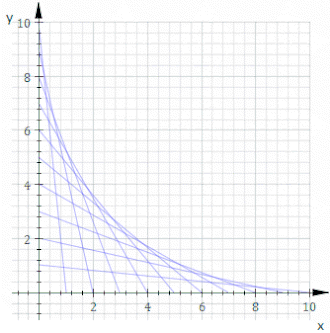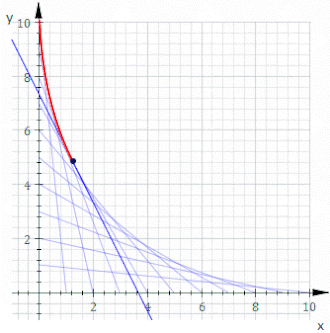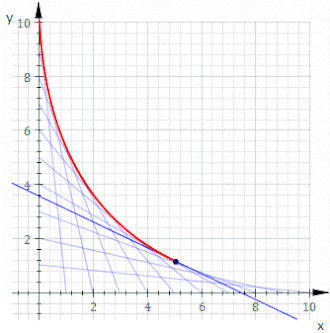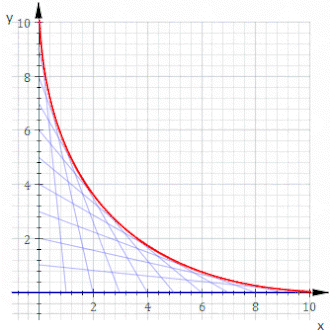
En indhylningskurve (engelsk: envelope) er i geometrien en kontinuer kurve, hvor hvert punkt til sammen tangerer alle medlemmer af en familie af kurver.

Definition

Enhver kurve i to dimensioner kan skrives som:

$y=f_t(x)$

hvor $x$ og $y$ er koordinater, og $t$ er et parameter for kurvefamilien. Den kan dog også skrives som en funktion lig nul:

$g_t(x,y)=0$

Tilsvarende må der være en funktion $F$ lig nul for indhylningskurven: Skabelon:NumBlk indhylningskurven gælder for alle værdier af $t$Skabelon:Ndashden skal dække hele familienSkabelon:Ndashså:

$F(x,y,t_1)=F(x,y,t_2)=0$

Deraf følger, at

$\frac{F(x,y,t_2)-F(x,y,t_1)}{t_2-t_1}=0$

Når $t_1$ går mod $t_2$, er dette definitionen på en differentialkvotient: Skabelon:NumBlk Ligning Skabelon:EquationNote og Skabelon:EquationNote definerer indhylningskurven.

Eksempel

I denne familie går hver linje mellem punkterne ($t$,0), (0,$k-t$). Her er $k=1$.

Inden for string art er det almindeligt at lade lige snore gå fra søm til søm for derved at skabe nye former.

I et simpelt tilfælde forbinder hver snor punkterne $(t,0)$ og ($0,k-t)$, hvor $k$ er en konstant, og $t$ er familiens parameter. Den lige linje er da givet ved:

$y=-\frac{k-t}{t}x+k-t$

Ved at trække $y$ fra findes $F$:

$F(x,y,t)=-\frac{kx}{t}-t+k+x-y=0$

Den afledte er da:

$\frac{\partial F(x,y,t)}{\partial t}=\frac{kx}{t^2}-1=0$

Af denne ligning følger det, at:

$t=\sqrt{kx}$

Dette indsættes i udtrykket for $F$, og $y$ isoleres:

$\begin{array}{cc}y=& -\frac{kx}{\sqrt{kx}}+x+k-\sqrt{kx}\\ y=& x+k-2\sqrt{kx}\\ y=& (\sqrt{x}-\sqrt{k}{)}^2\end{array}$

Dermed er indhylningskurven fundet.